How to Calculate the Volume of a Cylinder

When it comes to under­stand­ing 3D geom­e­try, the Vol­ume of a cylin­der is one of the most prac­ti­cal and wide­ly applic­a­ble con­cepts. Whether you’re a stu­dent tack­ling math prob­lems, an engi­neer design­ing stor­age tanks, or some­one cal­cu­lat­ing the capac­i­ty of a soda can, this top­ic plays a crit­i­cal role.

This blog is your com­pre­hen­sive guide to under­stand­ing the for­mu­la, cal­cu­lat­ing cylin­der vol­ume step-by-step, and explor­ing its real-world sig­nif­i­cance. We’ll also pro­vide prac­tice prob­lems and tips and even touch on advanced con­cepts for enthu­si­asts. Let’s get start­ed!

What Is a Cylinder?

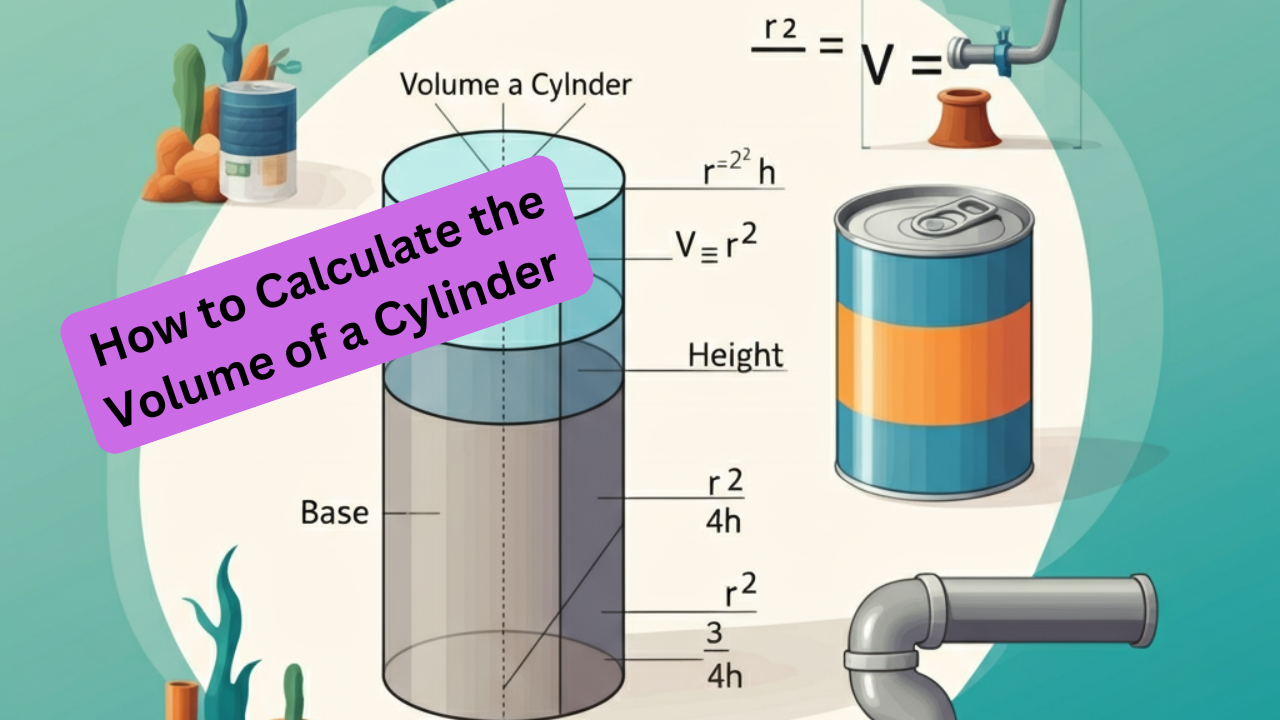
A cylin­der is a three-dimen­sion­al shape with two par­al­lel cir­cu­lar bases of equal size con­nect­ed by a curved sur­face. It is one of the sim­plest 3D shapes and is com­mon­ly seen around us.

Components of a Cylinder:

• Base: The cir­cu­lar sur­face at the top and bot­tom.
• Radius ®: The dis­tance from the cen­tre of the base to its edge.
• Height (h): The per­pen­dic­u­lar dis­tance between the two bases.

Key Difference From Other 3D Shapes:

• Unlike a cube or rec­tan­gu­lar prism with flat faces, a cylin­der has curved sur­faces.
• Unlike a cone, the cylinder’s two bases are the same size and par­al­lel.

Here’s a labelled dia­gram for easy under­stand­ing:

[Insert Dia­gram of a Cylin­der with Labeled Radius and Height]

The Formula for Volume of a Cylinder

The Vol­ume of a cylin­der is cal­cu­lat­ed using the for­mu­la:

V = πr²h

Where:

• V = Vol­ume of the cylin­der.
• π = Pi (approx­i­mate­ly 3.14159).
• r = Radius of the base.
• h = Height of the cylin­der.

Breaking Down the Formula:

• πr² rep­re­sents the area of the cir­cu­lar base.
• Mul­ti­ply­ing this area by the Height (h) gives the total space (or Vol­ume) the cylin­der occu­pies.

Step-by-Step Guide to Calculating Cylinder Volume

Fol­low these steps to cal­cu­late the Vol­ume of a cylin­der:

Example:

Find the Vol­ume of a cylin­der with:

• Radius (r) = 4 cm.
• Height (h) = 10 cm.

1. Note Down the For­mu­la  

V = πr²h

1. Sub­sti­tute Known Val­ues  

V = π × (4)² × 10

1. Cal­cu­late the Cir­cu­lar Base Area (πr²)  

V = π × 16 × 10

1. Mul­ti­ply by Height  

V = π × 160

1. Input the Val­ue of π (3.14159)  

V ≈ 502.65 cm³

The Vol­ume of the cylin­der is approx­i­mate­ly 502.65 cubic cen­time­tres.

You can also use online cal­cu­la­tors for quick­er results (we’ll list tools in the con­clu­sion).

Real-World Applications of Cylinder Volume

Under­stand­ing how to cal­cu­late the Vol­ume of a cylin­der has count­less prac­ti­cal uses. Here are a few:

• Every­day Use:
  • Deter­min­ing how much liq­uid a water tank can hold.
  • Mea­sur­ing the capac­i­ty of cylin­dri­cal con­tain­ers like cans or bot­tles.

• Con­struc­tion and Engi­neer­ing:
  • Cal­cu­lat­ing the Vol­ume of pipes dur­ing plumb­ing projects.
  • Design­ing stor­age tanks or silos.
• Man­u­fac­tur­ing:
  • Opti­miz­ing mate­r­i­al used in pro­duc­ing cylin­dri­cal objects.
• Sci­ence Exper­i­ments and Research:
  • Mea­sur­ing the dis­place­ment in cylin­dri­cal solids or flu­ids.

Tips and Tricks for Accurate Calculations

• Always use the same units for radius and height (e.g., meters, cen­time­tres). Con­vert them into con­sis­tent units if need­ed.
• If giv­en the diam­e­ter, remem­ber to divide it by 2 to find the radius.
• Show all steps when solv­ing prob­lems to avoid miss­ing key details.
• Use accu­rate val­ues of π (at least 3.14) for pre­cise results.
• Cross-check your answers using an online cal­cu­la­tor for con­fir­ma­tion.

Common Mistakes to Avoid:

• For­get­ting to square the radius (r²).
• Using incon­sis­tent units for radius and Height.
• Mix­ing up diam­e­ter and radius.

Advanced Topics

Once you’ve mas­tered the basics, explore these advanced con­cepts:

Hollow Cylinder Volume:

To cal­cu­late the Vol­ume of a hol­low cylin­der:

1. Sub­tract the small­er radius from the larg­er radius (out­er — inner).
2. Apply the for­mu­la for the remain­ing cylin­der.

Oblique Cylinders:

For tilt­ed or slant­ed cylin­ders, the Height used in the vol­ume for­mu­la is the per­pen­dic­u­lar Height, not the slant.

Using Calculus:

Inte­gra­tion is used to derive the for­mu­la for cylin­der vol­ume, enhanc­ing your under­stand­ing of geom­e­try and physics.

Surface Area:

The total sur­face area of a cylin­der can be cal­cu­lat­ed using:

Sur­face Area = 2πr² + 2πrh

This for­mu­la includes both bases and the curved sur­face.

Practice Problems

Put your knowl­edge to the test with these prob­lems:

1. Find the Vol­ume of a cylin­der with radius = 5 cm and height = 12 cm.
2. A pipe is hol­low, with an out­er radius = 7 m, an inner radius = 5 m, and a Height = 10 m. Cal­cu­late the Vol­ume of the mate­r­i­al used.
3. Dou­ble the radius of a cylin­der with ini­tial radius = 3 m and height = 8 m. How does its vol­ume change?

Answer Key:

1. V ≈ 942 cm³
2. V ≈ 376.99 m³
3. Vol­ume increas­es 4 times when the radius is dou­bled.

FAQ Section

How do I find the radius if I only know the diameter?  

Divide the diam­e­ter by 2 to find the radius.

What units should I use for volume calculations?  

Always ensure radius and Height are in the same units—Volume is typ­i­cal­ly expressed in cubic units (e.g., cm³, m³).

Can this formula be used for hollow cylinders?  

Yes, but you need to sub­tract the Vol­ume of the inner cylin­der from the out­er one.

How does the volume change if I double the radius?  

Dou­bling the radius increas­es the Vol­ume by 4 times (since r² is squared).

Where can I find online calculators for cylinder volume?  

Sites like Wol­fra­mAl­pha or apps like GeoGe­bra offer online vol­ume cal­cu­la­tors.

What is the difference between Volume and surface area?  

Vol­ume mea­sures the space inside a cylin­der, while sur­face area mea­sures the out­er sur­face.

How is the Volume of a cylinder used in engineering?  

It’s used for design­ing every­thing from stor­age tanks to pip­ing sys­tems.

Is the formula different for oblique cylinders?  

No, but ensure you use the per­pen­dic­u­lar Height, not the slant height.

Further Resources

Explore these math resources:

• “Geom­e­try Made Easy” by John Doe (Book)
• WolframAlpha’s Cylin­der Vol­ume Cal­cu­la­tor

Relat­ed post:

Pen­ta­gon shape-Definition,Properties,Types

20 cm to Inch­es – Easy Con­ver­sion Guide

Have ques­tions? Drop a com­ment below! 🚀