Square roots are fundamental in mathematics, bridging the gap between basic arithmetic and advanced problem-solving. While numbers like the square root of 4 may seem straightforward, exploring non-perfect squares like the square root of 8 introduces more complexity. This guide covers everything you need to know about the square root of 8, including its calculation, properties, and real-world applications.
Table of Contents
ToggleWhat Is the Square Root of 8?
The square root of 8 is the number which, when multiplied by itself, equals 8. Mathematically, it is expressed as:
The square root of 8 is an irrational number, meaning it cannot be expressed as a precise fraction and has a non-repeating, non-terminating decimal representation. Its approximate value is:
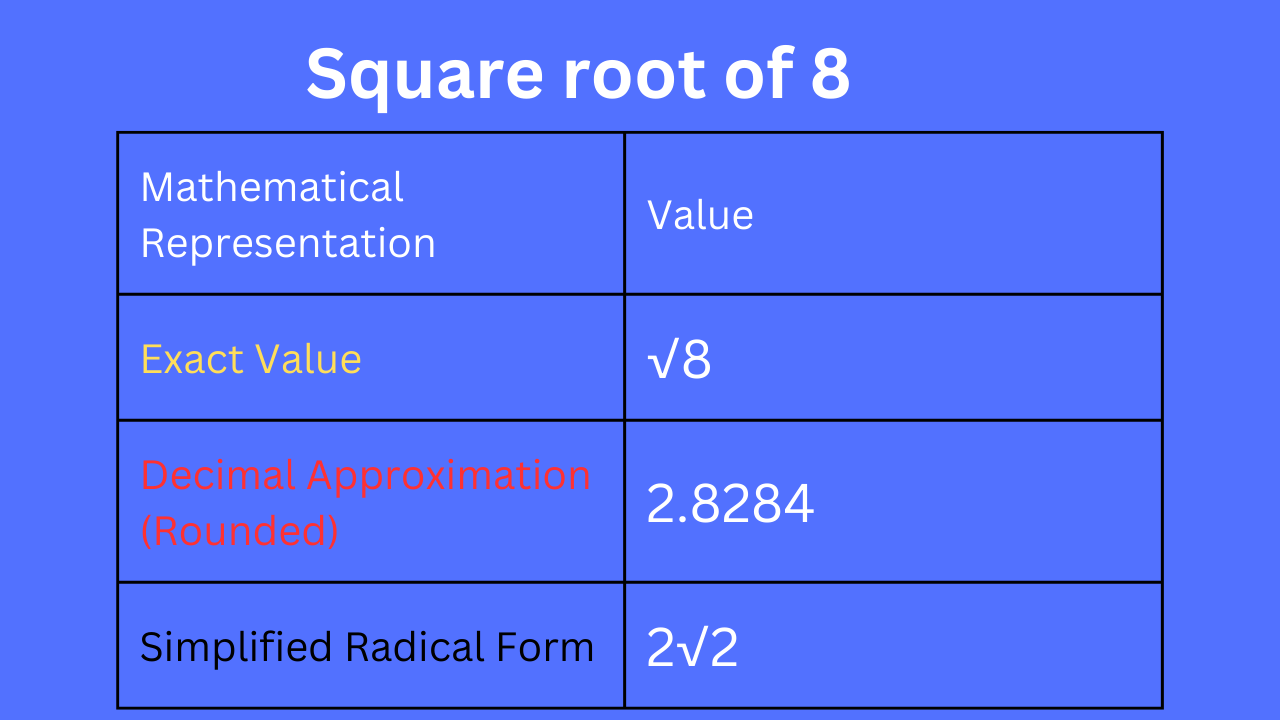
Mathematical Representations:
- Exact Value:
- Decimal Approximation: 2.8284
- Simplified Radical Form:
Why Are Square Roots Important?
Square roots are essential in various fields, including:
- Geometry (calculating diagonal lengths)
- Physics (vector magnitudes)
- Engineering (structural calculations)
- Finance (growth rate calculations)
Understanding the square root of 8 specifically helps in many real-world scenarios, as seen below.
How to Calculate the Square Root of 8
1. Prime Factorization Method
To simplify , break it into prime factors: Since one pair of twos can be taken out of the square root:
2. Approximation Using Perfect Squares
Find the nearest perfect squares around 8:
- Thus, lies between 2 and 3. Using a calculator:
3. Using a Calculator
Simply enter 8 and press the square root (√) function to get an accurate result.
4. Newton’s Approximation Method
Newton’s iterative formula helps approximate square roots: where , and is an initial guess (e.g., 3). This method refines results with each iteration.
| Mathematical Representation | Value |
|---|---|
| Exact Value | √8 |
| Decimal Approximation (Rounded) | 2.8284 |
| Simplified Radical Form | 2√2 |
Real-World Applications of the Square Root of 8
1. Geometry
- Diagonal of a Square: If a square has a side length of 2 units, its diagonal is units.
2. Physics
- Vector Magnitudes: Used in calculating the resultant force when two equal forces act perpendicularly.
3. Engineering
- Structural Designs: Engineers use in load calculations and material stress tests.
4. Computer Graphics
- Scaling and Distance Calculations: Square roots are used in 2D/3D transformations.
5. Finance
- Growth Rate Calculations: Square roots help in determining interest rates and investment returns.
Common Mistakes When Dealing with √8
- Ignoring Simplification: Always express in its simplest radical form .
- Confusing Exact and Approximate Values: 2.8284 is an approximation, not the exact value.
- Misapplying the Radical Symbol: , but some mistakenly write .
- Forgetting That √8 is Irrational: It cannot be written as a simple fraction.
Exploring Related Concepts
- Square Roots of Other Non-Perfect Squares (e.g., )
- Pythagorean Theorem (used in diagonal and distance calculations)
- Cube Roots (useful for higher-dimensional calculations)
FAQs About the Square Root of 8
1. What is the square root of 8?
The square root of 8 is , approximately 2.8284.
2. How do you calculate the square root of 8?
Using prime factorization, approximation with perfect squares, or a calculator.
3. Is the square root of 8 rational?
No, because its decimal representation is non-repeating and non-terminating.
4. Where is the square root of 8 used?
In geometry (diagonals), physics (vectors), engineering, graphics, and finance.
Forgetting to simplify, misapplying the radical, or confusing exact and approximate values.
Conclusion: Mastering the Square Root of 8
The square root of 8 is a fascinating mathematical concept that extends beyond numbers to real-world applications. Here’s a recap:
✅ Simplified Form:
✅ Decimal Approximation: 2.8284
✅ Real-World Uses: Geometry, physics, finance, and engineering
✅ Common Mistakes: Not simplifying, confusing approximations, and misapplying the radical
By understanding , you build a stronger foundation in mathematics and its practical uses. Keep exploring, practicing, and applying your knowledge to real-life problems!
Want to dive deeper? Explore related topics like the Pythagorean Theorem and cube roots to expand your math skills.
Related Posts
🔹 Understanding the Pentagon Shape: Definition & Properties
🔹 Easy Conversion Guide: 20 cm to Inches
Have questions? Drop a comment below! 🚀