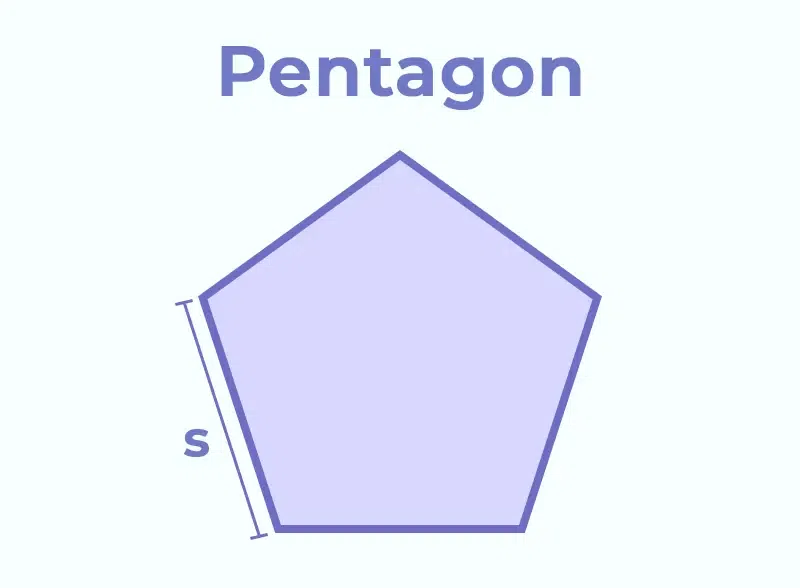
A pentagon is a five-sided polygon with five angles. The word “pentagon” comes from the Greek words “penta,” meaning five, and “gon,” meaning angle. As one of the basic types of polygons, a regular pentagon (where all sides and angles are equal) has interior angles that add up to 540 degrees.
In geometry, we explore a variety of shapes, especially those formed by straight lines and angles—these are known as polygons. A polygon is a two-dimensional closed figure made up of line segments. Common examples include:
- Triangle (3 sides)
- Quadrilateral (4 sides)
- Pentagon shape (5 sides)
- Hexagon (6 sides)
- Heptagon (7 sides)
- Octagon (8 sides), and so on.
In this article, we’ll focus on the pentagon shape—a five-sided polygon. You’ll learn what defines a pentagon, how it looks, its sides and angles, key properties, and how to calculate both its perimeter and area using simple formulas.
| Types of Pentagon |

What Is a Pentagon Shape?
A pentagon is a type of polygon that has five sides and five angles. The term “pentagon” comes from the Greek words “penta” meaning five and “gonia” meaning angle. In a pentagon, each side connects to the next, forming a closed five-sided figure.
So, the total number of sides in a pentagon shape is 5.
To visualize a Pentagon, think of a home plate on a baseball field or the iconic Pentagon building in Washington, D.C.—both are excellent representations.
| Understanding the Pentagon Shape |
Shape of a Pentagon
The Pentagon’s unique geometry makes it easily recognizable. It consists of:
- Five sides can either be equal (in a regular pentagon) or unequal (in an irregular pentagon).
- Five vertices (corners) where the sides meet.
- Five interior angles, whose sum always equals 540 degrees in both regular and irregular cases.
Here’s a simple diagram of a regular pentagon, showing its equal sides and angles—a great reference point for understanding its symmetry.
Regular vs. Irregular Pentagons
Regular Pentagon
A regular pentagon is balanced and symmetrical. All five sides are of equal length, and all internal angles are congruent, measuring 108 degrees each. These pentagons are frequently used in design, patterns, and architecture due to their visual appeal.
Irregular Pentagon
An irregular pentagon lacks symmetry. Its sides and angles can vary in length and size. Irregular pentagons are more common in nature and functional designs—like the shape of some tools or fixtures.
Convex vs. Concave Pentagons
Convex Pentagon
A convex pentagon is simple; none of its interior angles exceed 180 degrees, and its vertices point outward. Most pentagons we encounter, such as the Pentagon building, are convex.
Concave Pentagon
On the other hand, a concave pentagon has at least one internal angle greater than 180 degrees, giving it a “caved-in” appearance. These shapes are less common but can be seen in specialized designs or artistic creations.
Properties of the Pentagon Shape
Here are the fundamental properties of pentagons that define their geometry:
- Sides: Five straight sides.
- Angles: The sum of all interior angles is always 540 degrees.
- Diagonals: A pentagon has five diagonals, which connect non-adjacent vertices.
- Symmetry: Regular pentagons exhibit symmetry, enhancing their aesthetic appeal.
How to Calculate the Area of a Pentagon
The formula for calculating the area of a regular pentagon involves its side length (s) and apothem (a):
Area = (5 × s × a) / 2
Step-by-step guide:
- Measure the side length of the Pentagon.
- Measure the apothem (the perpendicular distance from the center to the midpoint of any side).
- Plug both values into the formula.
Example Calculation:
If a regular pentagon has a side length of 6 cm and an apothem of 5 cm, the area is calculated as follows:
Area = (5 × 6 × 5) / 2 = 75 cm²
For irregular pentagons, you’ll need to divide the shape into smaller triangles, calculate their areas individually, and sum them up.
How to Calculate the Perimeter of a Pentagon
The perimeter of a pentagon is the sum of its five sides.
For a regular pentagon:
Perimeter = 5 × side length
For an irregular pentagon:
Add the lengths of all five sides.
Example Calculation:
If a regular pentagon has a side length of 8 cm, the perimeter equals 5 × 8 = 40 cm.
Fascinating Examples of Pentagon Shapes
Pentagons are surprisingly common in both design and nature. Here are some notable examples:
- The Pentagon Building: The United States Department of Defense headquarters in Washington, D.C., is one of the most famous real-world examples of a Pentagon shape.
- Baseball Home Plate: The iconic shape of a baseball home plate is a pentagon.
- Starfish: Certain species of starfish exhibit a natural pentagonal shape.
- Snowflakes: Some snowflakes show pentagonal symmetry as part of their intricate designs.
- Nuts and Bolts: Select specialty nuts and bolts that have pentagonal designs for added functionality.
Unique Pentagon Variants
Equilateral Pentagon
An equilateral pentagon has all sides of equal length but may have unequal angles. It’s similar to a regular pentagon but with varying angles breaking the symmetry.
Cyclic Pentagon
A cyclic pentagon can be inscribed within a circle, with all its vertices lying on the circle’s circumference. This unique property is often employed in architectural and design projects to enhance visual appeal.
Frequently Asked Questions (FAQs)
What shapes make up a pentagon?
A pentagon is a simple, two-dimensional shape with five straight sides and five angles. All of its angles together add up to 540 degrees. Just like familiar shapes such as triangles, squares, and circles, a pentagon lies flat on a surface—making it a 2D shape. Whether all sides are equal or not, as long as it has five sides and five angles, it’s a pentagon!
What Is a Pentagon? And Where Do We See It in Real Life?
A pentagon is a five-sided shape often found not just in geometry class but all around us in the real world. Its five sides and five angles make it both simple and fascinating—and surprisingly common in everyday life. Here are a few interesting places where pentagon shapes appear:
- Architecture & Design: Many modern and traditional buildings incorporate pentagon-shaped patterns or structures in their floor plans, windows, or decorative elements.
- Baseball Home Plate: The iconic shape of the home plate on a baseball field is a perfect example of a practical pentagon used in sports.
- Soccer Ball Panels: While most people think of hexagons on a soccer ball, there are also pentagons stitched into its surface, giving it that classic patterned look.
Other cool examples include school crossing signs, starfish, some tea bags, okra slices, and even the shapes of certain flowers.
What Is a Pentagon? And Where Do We See It in Real Life?
A pentagon is a five-sided shape often found not just in geometry class but all around us in the real world. Its five sides and five angles make it both simple and fascinating—and surprisingly common in everyday life. Here are a few interesting places where pentagon shapes appear:
- Architecture & Design: Many modern and traditional buildings incorporate pentagon-shaped patterns or structures in their floor plans, windows, or decorative elements.
- Baseball Home Plate: The iconic shape of the home plate on a baseball field is a perfect example of a practical pentagon used in sports.
- Soccer Ball Panels: While most people think of hexagons on a soccer ball, there are also pentagons stitched into its surface, giving it that classic patterned look.
Other cool examples include school crossing signs, starfish, some tea bags, okra slices, and even the shapes of certain flowers.
Is a 5 sided shape a pentagon?
In geometry, a pentagon is a shape with five sides and five angles. The name comes from the Greek words pente meaning “five” and gonia meaning “angle,” which together describe this classic five-sided polygon.
Why the Pentagon Shape Matters ?
The Pentagon is far more than a five-sided geometry lesson—it bridges the gap between mathematics, design, and the natural world. Understanding its structure and applications enhances our appreciation for patterns, symmetry, and shapes in everything from architecture to nature.
Take a fresh look at the pentagon shape, and you may discover that its five sides hold countless possibilities for exploration and creativity.
Read also : 20 cm to Inches – Easy Conversion Guide
- A pentagon has 5 sides and 5 angles.
- The sum of interior angles is always 540°.
- Regular pentagons have equal sides and angles (108° each).
- Seen in nature (e.g., starfish, okra).
- Used in architecture and design.
- Found in sports (e.g., baseball plate).
- The U.S. Pentagon building is its famous example.